
大阪大学卒/塾講師歴5年/家庭教師歴6年/E判定から阪大へ逆転合格/勉強法を教えた生徒は「2週間で苦手教科が27→73点」「定期テストの5教科合計200点以上アップ」「E判定から3ヶ月で逆転合格」など、劇的な成績アップを多数達成/著書『成績があがる中学生の勉強法』『だから勉強ができない20の考え方』




「数学が難しい」「数学は嫌い」と思っている中学生はとても多いです。数学ができないと「才能がない」と思ってしまいがちですよね。
しかし、数学は「勉強すれば必ずできるようになる科目」です。苦手になってしまうのは「原因」があります。それを潰せばOKです。
数学が苦手になってしまう5つの原因と得意にするための勉強法を詳しく紹介します!








数学ができない理由は「才能がないから」ではなく、「勉強方法が間違っているから」です。
間違っている部分、つまり、「数学ができない原因」を潰せば誰でも得意にできます。
中学生が数学を苦手になってしまう原因の多くは次の5つです。
順に解説します。
1つ目のよくある原因は「計算問題が定着できていないこと」です。
数学が苦手な人でも「計算問題くらいはできる」と思っている人が多いですが、実は「キチンとできていない」という場合がほとんどです。
「公式を見ながら」計算問題を解いて、「できる」と思い込んでしまっています。
計算をできるようにするためには、公式を見ないで、テストと同じ状況で正解できるようにトレーニングすることが大切です。
また、計算問題ができないと、他の単元の問題もできなくなってしまいます。
例えば、中学1年生で習う「方程式」の計算問題です。
もし、方程式の計算問題ができないと、その次に習う「y=x」といったグラフの問題や、図形で角度を求める応用問題、2年生の連立方程式など、「方程式の計算」を使って解く問題が全てできなくなってしまいます。
「グラフが苦手」と言っている生徒も、実は「問題で使う方程式の計算ができていなかっただけ」ということがよくあります。
数学の基礎となる「計算問題」を苦手にすると、他の単元までできなくなってしまうので、計算分野に苦手意識がある場合は早めに復習をして克服しておきましょう。
上記と同じ理由ですが、「小学生の算数ができていないこと」も数学が苦手になる原因です。
小学生時代に算数が苦手だった人は、中学生になっても「算数」の部分でつまづいてしまっていることが多いです。
「中学生になったから自動的に小学生の範囲もできるようになる」なんてことはありえません。何事も、できるようになるにはトレーニングが必要です。
特につまづく人が多いのが「分数」の計算です。
6÷3=2
などの「整数の割り算」はできる人の方が多いですが、
262÷12
のような答えが分数になるような計算だと、苦手意識を持っている中学生は多いです。
分数は、中学校の範囲では「できることが当然」として使われます。
分数ができない、もしくは苦手意識がある状態だと、これらの計算が全てできなくなります。
中学数学がどうしてもできない時、場合によっては小学校の計算ドリルまで戻ることも大切な復習です。
3つ目の原因は「背伸びして応用問題を解こうとしていること」です。
応用問題に挑戦したものの、



と思ってしまうパターンです。真面目に勉強しているのに、数学に苦手意識を持ってしまう中学生に多い傾向ですね。
応用問題では、新たな公式などが必要になることはありません。全て習っている内容で解けるように構成されています。
だからこそ、応用問題を解くには、「様々な基本問題の解き方や考え方をしっかりと習得していること」が必要です。
それなのに、背伸びして解こうとすると、当然できないので、不要な苦手意識を持ってしまいます。
応用問題は、基本問題をしっかりと定着させた状態で挑戦しましょう。
計算ミスが多くて失点してしまう子によくある原因が「暗算で解こうとしまっていること」です。
例えば、
2x-6=12
という方程式の計算です。
答えは「x=9」ですが、「ミス」が起こってしまうことがよくあります。
解く過程を「全て」書くと次のようになります。
2x-6=12
2x=12+6(左辺の-6を移項)
2x=18(右辺の12+6を計算)
x=9(両辺を2で割って解を得る)
途中式を書くと基本的な問題ですが、全てを頭の中でやってみると、格段に難しくなってしまうんです。
例えば「-6の移項でマイナスをプラスに変えるのを忘れる」といったミスです。
2x-6=12
2x=12–6(移項で符号を変えるのを忘れている!)
2x=6(気づかずに計算)
x=3(答えは間違いに)
このミスは、
という3ステップの計算を一気に暗算でやろうとしてしまっていることが原因です。
誰でも一時的に覚えられることは限られています。そのため、一度に3つのことをやろうとしてしまうと、どこか抜けてしまったり、注意が及ばないことがあり、ミスにつながってしまいます。
このようなミスは面倒くさがらずに、「しっかり途中式を書くだけ」で解消できます。
計算ミスが多い人は「暗算」で考えようとしすぎていないか、注意してみることが大切です。
応用問題に苦手意識がある人によくある原因として、「解き方全てを自分で考えようとしていること」があります。
基本問題だけを覚えて、あとは思考力で勝負しようとしてしまっています。



と驚く生徒も多いですが、実は応用問題が解ける人のほとんどは
という理由がほとんどです。
例えば、次のような面積を求める問題です。
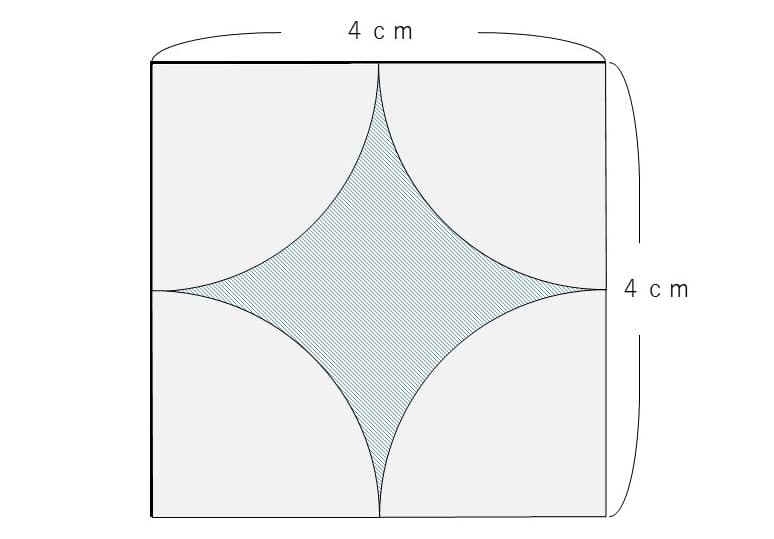

このような問題を初めて解く人は次のように考えます。



は?見たことない図形だ



こんな面積の公式習ってないけど、どうやって解けばいいの?



無理・・・わからない
全く解き方を思いつくことができません。
しかし、次のような問題を解いたことがある生徒は考え方が変わります。
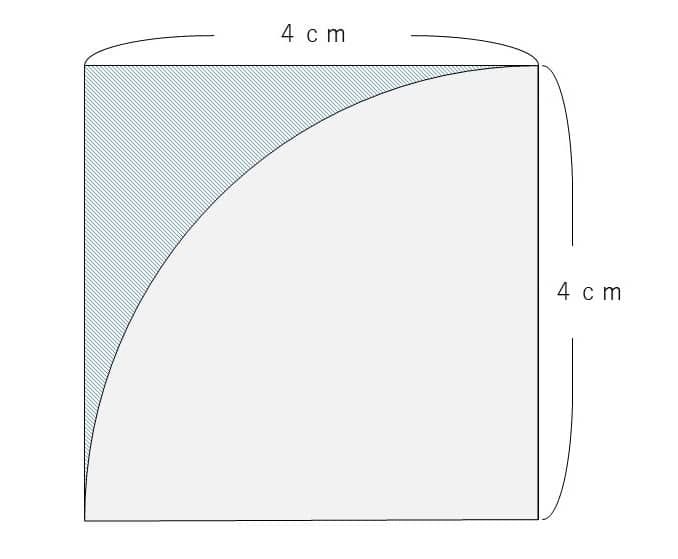




難しそうな問題だけど、この前やった基本問題に似ているな



もしかしたらこの問題も同じように解くのかもしれない!
「初めて解く人」よりも「似た問題を知っている人」の方が解けそうですよね。
「補助線を引く問題」を解いた経験があれば次の「正しい解き方」をきちんと思いつけそうです。
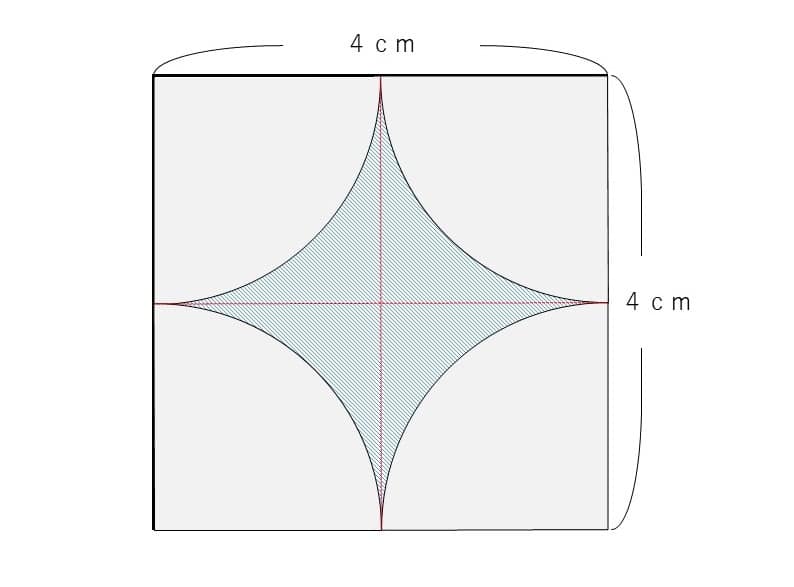

応用問題はこのように「基本問題の知識を組み合わせる経験」でできるようになっていきます。
つまり、できる人はゼロから自分の頭で考えるのではなく、似た問題の解き方を参考にしながら考えているんです。



応用問題がニガテ
と思っている人は、できなかった応用問題の解説を自分の知識にしていくことで、応用問題ができるようになります。






上記で数学が苦手になる原因を5つ紹介しましたが、「どれも当てはまっているような気がして、何から手をつけたらいいかわからない」という中学生も多いと思います。
そこで、塾でもよく使われる「数学の苦手克服勉強法」をステップごとに紹介します!
まずは不安な単元まで戻って復習しましょう。
数学は積み重ねの教科のため、不安な単元を残しておくと、今の単元の勉強がますます進めづらくなります。



そんな時は、今回の定期テストに関連する単元だけに絞って復習しましょう。
例えば、「計算分野」が今回のテスト範囲なら、復習も「計算分野」だけでOKです。
もし、「以前の範囲を復習する必要があるかどうか」が判断できない場合は、
を考えてみましょう。もし、「基本的な問題がわからない」という場合は戻って復習するほうが効率的に勉強が進められます。
これまでの復習ができたら、次は「基本問題」を確実にできるようにします。
「公式を見ながら」ではなく、「何も見なくてもスラスラ解ける」というレベルまで基本問題だけをやり込みます。このステップでは、応用問題は飛ばしてOKです。
覚え方の基本は5回以上解き直すことです。
全教科に共通する覚え方なので、次の記事で詳しく紹介しています。




基本問題がスラスラ解けるようになったら、いよいよ応用問題にチャレンジしていきます。
応用問題は考え方が難しいため、初めて解く場合は



と悩んでしまうことがほとんどです。
まずは、例題などにチャレンジして、解説で「考え方」を学ぶことがスタートになります。
わからない応用問題の解説を読んで理解し、しっかり解き直して覚え、「応用問題の考え方」を吸収していくことが大切です。そうすることで、どんどん応用問題を解くための実力上がっていきます。
上記ステップでしっかりトレーニングすることで、数学の実力は面白いほど伸びていきます。
数学は積み重ねの教科です。
苦手な人は必ずどこかのタイミングで「積み残し」があります。それをつぶせば必ず苦手は克服できます。
数学のトレーニングのためのおすすめ問題集は下記記事でも詳しくまとめていますので、よろしければご参考にしてください。


また、数学の苦手克服をしたい場合は、「通信教育教材を利用すること」もおすすめの勉強法です。
上記の「正しい勉強法のステップ」が通信教育の「学習カリキュラム」として自動的に組み込まれているので、安心してトレーニングを続けることができます。
下記で具体的なおすすめ教材を紹介していますので、学習方法に不安があるご家庭は無料体験セットから試してみることをおすすめします。


数学は才能ではなく、正しく勉強すれば誰でもできるようになります。
ぜひこの記事で紹介した勉強法で、実力をアップさせてください!



がんばっているのに、子どもの点数があがらない…



勉強法が間違っているだけです。
やり方を正せば、短期間でも面白いほど上がります!
がんばっているのに成績が上がらない原因は、お子様の頭が悪いわけでも、才能がないわけでもありません。
「間違った勉強法」で勉強をしてしまってるだけです。
やり方がズレていると、どれだけがんばっても結果につながらないんです。
私が塾講師や家庭教師として「勉強のやり方を正した生徒たち」は、次のような圧倒的な成績アップができました。
みんな「勉強が苦手…」と悩んでいた生徒でした。でもその原因は「間違った勉強法でやっていただけ」なんです。
勉強は才能ではなく、やり方で劇的に変わるんです。
実は、この勉強法は今すぐご家庭でも真似することができる方法です。でも、多くの子どもたちは間違った勉強法で努力してしまっています。この方法を知らずに、「勉強が苦手」と悩みながら頑張るのは、とてももったいないことだと思っています。
だから、「お子様の成績アップを願う保護者の皆さま」のために、「正しい勉強法」を徹底解説する無料の勉強法講座を開講しています。
LINEで、私が塾でも教えていた勉強法を出し惜しみなく解説したLINE限定の無料7日間講座をお送りしています!
これまで5000名以上の保護者さま、1000名以上の生徒さんに参加いただいて、「過去最高点だった!」「五教科で100点もあがった!」という成績変化のお声もたくさんいただいています。


勉強ができないのは才能の問題ではありません。ただ、「正しく勉強する方法」を知らないだけなんです。
私は確信を持って、そう言えます。
なぜなら、私自身がそれを身をもって経験してきたからです。
勉強が伸び悩むのは才能ではなく、やり方が間違っているだけです。
テクニック的に勉強して、テストの点数や合格だけとっても、将来に役に立ちません。
本質的なやり方で正しく勉強できれば、成績は伸び、受験にも合格でき、何よりも将来に活きる力が身につきます。
勉強は才能ではなく、やり方の問題です。正しくやれば、誰でも面白いほど伸びます。
具体的にどうすれば勉強法を正せるのかを徹底的にご紹介します。お子様の成績アップのために、ぜひご活用ください。
今なら、登録いただいた方へ
を無料プレゼント中です!
多くの生徒の成績を上げたノウハウがギュッと凝縮されているマニュアルのため、ぜひお受け取りください!